HFHE Key Sharding

The scheme and description below provide a visual example of how we divide keys and distribute them across nodes. The bootstrapping algorithm based on hypergraphs is not presented here, and all key features are generalized. The details of these important algorithms will be explained in subsequent articles.

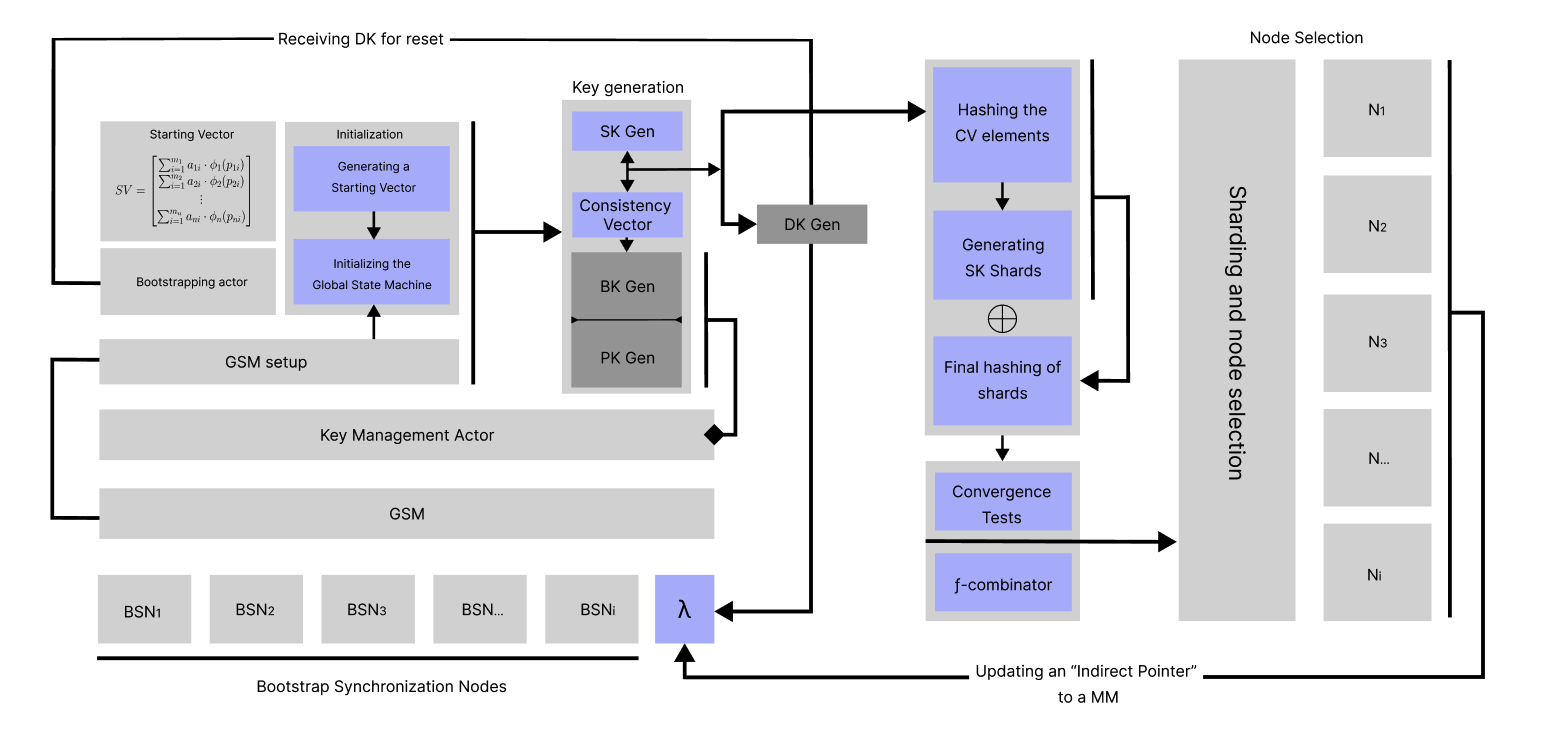
Schematic diagram of key sharding

1. Initialization The process of setting up the Global State Machine (GSM) and generating the Starting Vector.

2. Starting Vector (SV) The initial vector derived from key components, used as the foundation for further cryptographic processes.

3. Key Generation

   • SK Gen Secret Key Generation process where the starting vector is hashed and transformed into the secret key.

   • Consistency Vector A transformation of the Secret Key that is used in the generation of other keys.

   • DK Gen Decryption Key Generation where the Decryption Key is derived from the Secret Key and Consistency Vector.

   • BK Gen Bootstrapping Key Generation for noise reduction in ciphertexts.

   • PK Gen Public Key Generation for encryption, which will be shared with users for secure communication.

4. Hashing the CV elements The process of hashing elements of the Consistency Vector for shard generation.

5. Generating SK Shards The operation where the Secret Key is split into shards for distribution.

6. Final hashing of shards The last step of hashing each shard for additional security before distribution.

7. Convergence Tests Tests to ensure that the shards can be recombined to recover the original Secret Key.

8. ƒ-combinator A function that prepares sharded keys for node allocation, confirming their integrity and recoverability to ensure the original Secret Key can be accurately reconstructed from the shards.

9. Node Selection The process of selecting nodes for shard distribution, ensuring data resilience and security.

10. GSM The Global State Machine which maintains the state of the system.

11. Bootstrapping actor The entity responsible for initiating the bootstrapping process.

12. Key Management Actor The component that manages the lifecycle of keys including generation, rotation, and retirement.

13. Bootstrap Synchronization Nodes Nodes responsible for synchronizing the bootstrapping process across the system.

14. Receiving DK for reset The step where the Decryption Key is received for the purpose of resetting or reducing noise in the ciphertexts.

15. Updating an "Indirect Pointer" to a MM The action of updating an indirect pointer within the Global State Machine.

Description of the methods used

The Starting Vector is a structured array where each element is a sum of products of coefficients and the respective transformed parameters.

$$SV = \left[ \begin{array}{c} \sum_{i=1}^{m_1} a_{1i} \cdot \phi_1(p_{1i}) \\ \sum_{i=1}^{m_2} a_{2i} \cdot \phi_2(p_{2i}) \\ \vdots \\ \sum_{i=1}^{m_n} a_{ni} \cdot \phi_n(p_{ni}) \end{array} \right]$$

Keys generation process

Secret Key Generation

The Secret Key is generated by hashing the XOR-ed result of each Starting Vector element $SV_i$. after applying an S-box transformation and an additional XOR with coefficient $a_i$.

$$SK = \text{Hash}\left( \bigoplus_{i=1}^{n} \text{Sbox}\left( \text{Hash}(SV_i) \oplus a_i \right) \right)$$

Consistency Vector Generation

The Consistency Vector is created by transforming each element of the Secret Key through multiplication with a corresponding large prime and addition of a shift factor.

$$VC = \left\{ (SK_i \times \text{large\_prime}_i) + \text{shift}_i \right\}_{i=1}^{n}$$

Bootstrapping Key Generation

The Bootstrapping Key is obtained by XOR-ing all elements of the Consistency Vector, used in the noise reduction process during decryption.

$$BK = \bigoplus_{i=1}^{n} VC_i$$

Public Key Generation

The Public Key is derived by applying a modular operation to each element of the VC, followed by an addition of an offset, then combining the results using XOR.

$$PK = \bigoplus_{i=1}^{n} \left( \text{Mod}(VC_i, \text{mod\_val}_i) + \text{offset}_i \right)$$

Decryption Key Generation

The Decryption Key is generated by hashing the combined value of the Consistency Vector, the Secret Key, and the product of VC with a large prime, using the Blake 3 hash function for high security.

$$DK = \text{BLAKE3}\left( VC \oplus SK \oplus \left( VC \cdot \text{large\_prime} \right) \right)$$

Sharding and node selection

Hashing the Consistency Vector Elements

Each element of the Consistency Vector is hashed using the Blake 3 cryptographic hash function, taking corresponding elements of the Secret Key as input.

$$VC_i = \text{BLAKE3}(SK_i), \quad \text{for } i = 1, 2, \ldots, n$$

Generating SK Shards

Secret Key shards $SK_{shard}$ are generated by hashing the XOR of each Consistency Vector element $VC_i$ with a unique salt $salt_i$ using Blake 3, ensuring unique and secure sharding.

$$SK_{shard_i} = \text{BLAKE3}(VC_i \oplus salt_i), \quad \text{for } i = 1, 2, \ldots, n$$

Final Hashing of Shards

The final hash of each Secret Key shard $SK_{shard}$ is computed using Blake 3 to provide an additional layer of security, resulting in the final shard $SK_{final}$ ready for distribution.

$$SK_{final_i} = \text{BLAKE3}(SK_{shard_i}), \quad \text{for } i = 1, 2, \ldots, n$$

Node selection

The final selection of the node $Node_i​$ for each $i$ is based on the highest calculated value from the given expression.

$$Node_i = \underset{\substack{j=1,\ldots,N \\ i = 1, 2, \ldots, n}}{\mathrm{argmax}} \left( \sum_{k=0}^{4} C_k \cdot f_j^{(k)}(k) + \int_{a_j}^{b_j} g_j(x) \, dx + \sum_{\substack{p=0 \\ p \neq k}}^{4} h_{jp}(C_k, C_p) \right)$$

The node selection is determined through an optimization process that identifies the node with the maximal value of a predefined evaluative function, ensuring an optimal choice based on specified criteria for each index $i$.

Some critical elements such as the ƒ-combinator and Hypergraph Bootstrapping, key management actors, bootstrap node management actors, and noise level assessment are addressed in separate articles.